В лекциях по истории философии МФТИ лектор В. Лега рассказывает, что философия Платона и Аристотеля противопоставляются как разные школы, принципиально отличающиеся друг от друга. Однако на самом деле Аристотель развивает идеи Платона и Сократа. В сердцевине его учения лежат "идеи" Платона.
Сечение Дедекинда: иррациональность √2
Сечение Дедекинда для √2 определяет разбиение множества рациональных чисел на два класса:
A = {r ∈ ℚ: r < √2} — числа, меньшие √2 (синий)
A' = {r ∈ ℚ: r > √2} — числа, большие √2 (красный)
Увеличивайте масштаб, чтобы увидеть, как рациональные числа приближаются к √2 с обеих сторон, но никогда не достигают его точно.
Лучшие рациональные приближения к √2
| Дробь | Десятичная запись | Близость к √2 | Сторона |
|---|
О сечении Дедекинда и иррациональности √2
Ключевая особенность сечения для √2: сколько бы мы ни "увеличивали" область около √2, всегда будет оставаться "дырка", которую невозможно заполнить рациональным числом.
Доказано, что √2 иррационально — его нельзя представить в виде отношения целых чисел p/q. Рациональные числа могут приближаться к √2 сколь угодно близко, но никогда не будут равны ему точно.
Последовательность наилучших приближений к √2 можно получить из разложения в цепную дробь: [1; 2, 2, 2, ...], что даёт последовательность дробей: 1/1, 3/2, 7/5, 17/12, 41/29, ...
а) А ⊂ А б) если А ⊂ В и В ⊂ С, то А ⊂ С;
в) А = В, если и только если А ⊂ В и В ⊂ А.
Для того, чтобы множества были равны необходимо, чтобы по определению равенства множества состояли из одних и тех же элементов. По определению подмножеств А ⊂ В тогда, когда любой х множества А содержится в В. Для равенства одного этого не достаточно, так как В может быть больше, чем А.
И если одновременно с тем, что А ⊂ В и В ⊂ А, тогда А = В и В = А.
Доказательство равенства основывается на определении 1, в котором говорится, что множества равны тогда, когда они состоят из одних и тех же элементов: любой элемент множества A принадлежит множеству B и любой элемент множества B принадлежит множеству A.
1) A∪B ⊂ B∪A ;
2) B∪A ⊂ A∪B.
1. Предположим, что A∪B ⊄ B∪A. В таком случае будет существовать такой x, что x ∈ A∪B
и x∉ B∪A. По определению объединением множеств A и B (обозначение: A∪B) называется множество, состоящее из таких x, что x ∈ A или x ∈ B. Если x ∈ A, то по определению объединения x ∈ B∪A. Если x ∈ B, то по определению объединения x ∈ B∪A. Мы пришли к противоречию: x ∈ B∪A и одновременно x∉ B∪A. Следовательно A∪B ⊂ B∪A.
2. Аналогично доказывается второе включение B∪A ⊂ A∪B. Предположим противное: B∪A ⊄ A∪B. Тогда должен существовать элемент x такой, что: x ∈ B∪A и x ∉ A∪B. Но если x ∈ B ∪ A, то по определению объединения: x ∈ B или x ∈ A. Если x ∈ B, то по определению объединения x ∈ A∪B. Если x ∈ A, то по определению объединения x ∈ A∪B. В любом случае получаем x ∈ A∪B. Противоречие: x ∈ A∪B и x ∉ A∪B одновременно. Значит, предположение неверно и B∪A ⊄ A∪B.
Так как доказаны оба включения: A∪B ⊂ B∪A и B∪A ⊂ A∪B, то по определению о равенстве множеств: A∪B = B∪A.
Доказательство будем строить аналогично доказательству A∪B = B∪A.
Множество A∩B равно множеству B∩A тогда и только тогда, когда:
1) A∩B ⊂ B∩A ;
2) B∩A ⊂ A∩B.
Докажем, что: 1) A∩B ⊂ B∩A.
Предположим, что A∩B ⊄ B∩A. Тогда будет существовать хотя бы один x такой, что x ∈ A∩B и x ∉ B∩A. По определению пересечения, x ∈ A∩B означает, что x ∈ A и x ∈ B. Тогда, по определению B∩A, раз x ∈ B и x ∈ A, отсюда следует, что x ∈ B∩A. Мы пришли к противоречию: x ∈ B∩A и одновременно x∉ B∩A. Следовательно A∩B ⊂ B∩A.
Докажем, что: 1) B∩A ⊂ A∩B.
Предположим, что B∩A ⊄ A∩B. Тогда будет существовать хотя бы один x такой, что x ∈ B∩A и x ∉ A∩B. По определению пересечения, x ∈ B∩A означает, что x ∈ B и x ∈ A. Тогда, по определению A∩B, раз x ∈ A и x ∈ B, отсюда следует, что x ∈ A∩B. Мы пришли к противоречию: x ∈ A∩B и одновременно x∉ A∩B. Следовательно B∩A ⊂ A∩B.
Так как доказаны оба включения: A∩B ⊂ B∩A и B∩A ⊂ A∩B, то по определению о равенстве множеств: A∩B = B∩A.
Доказательство иллюстрирует свойство ассоциативности операции объединения множеств. Ассоциативность объединения означает, что порядок группировки скобок не влияет на результат. Для доказательства требуется показать два включения:
- A∪(B∪C) ⊂ (A∪B)∪C;
- (A∪B)∪C ⊂ A∪(B∪C).
1. Если х ∈ A, то по определению объединения х ∈ A∪B, тогда х ∈ (A∪B)∪C;
2. если х ∉ А, то х ∈ B∪C, тогда:
2.а. если х ∈ В, то х ∈ A∪B, тогда х ∈ (A∪B)∪C
2.б. если х ∈ С, то х ∈ (A∪B)∪C.
Во всех случаях A∪(B∪C) ⊂ (A∪B)∪C.
Шаг 2. (не буду расписывать полностью как первый шаг, ведь принцип и так понятен) Рассмотрим левую часть: (A∪B)∪C. Что это значит? Это значит, что любой произвольный элемент х ∈ A∪B или х ∈ C. Если х ∈ A∪B, то по определению объединения х ∈ (A∪B)∪C, если х ∉ А∪B, то х ∈ C, тогда х ∈ (A∪B)∪C. Следовательно, во всех случаях (A∪B)∪C ⊂ A∪(B∪C).
Доказательство иллюстрирует свойство ассоциативности операции объединения множеств. Ассоциативность объединения означает, что порядок группировки скобок не влияет на результат. Для доказательства требуется показать два включения:
- A∩(B∩C) ⊂ (A∩B)∩C;
- (A∩B)∩C ⊂ A∩(B∩C).
Шаг 2. Производится аналогично. В конечном итоге мы получаем, что A∩(B∩C)=(A∩B)∩C.
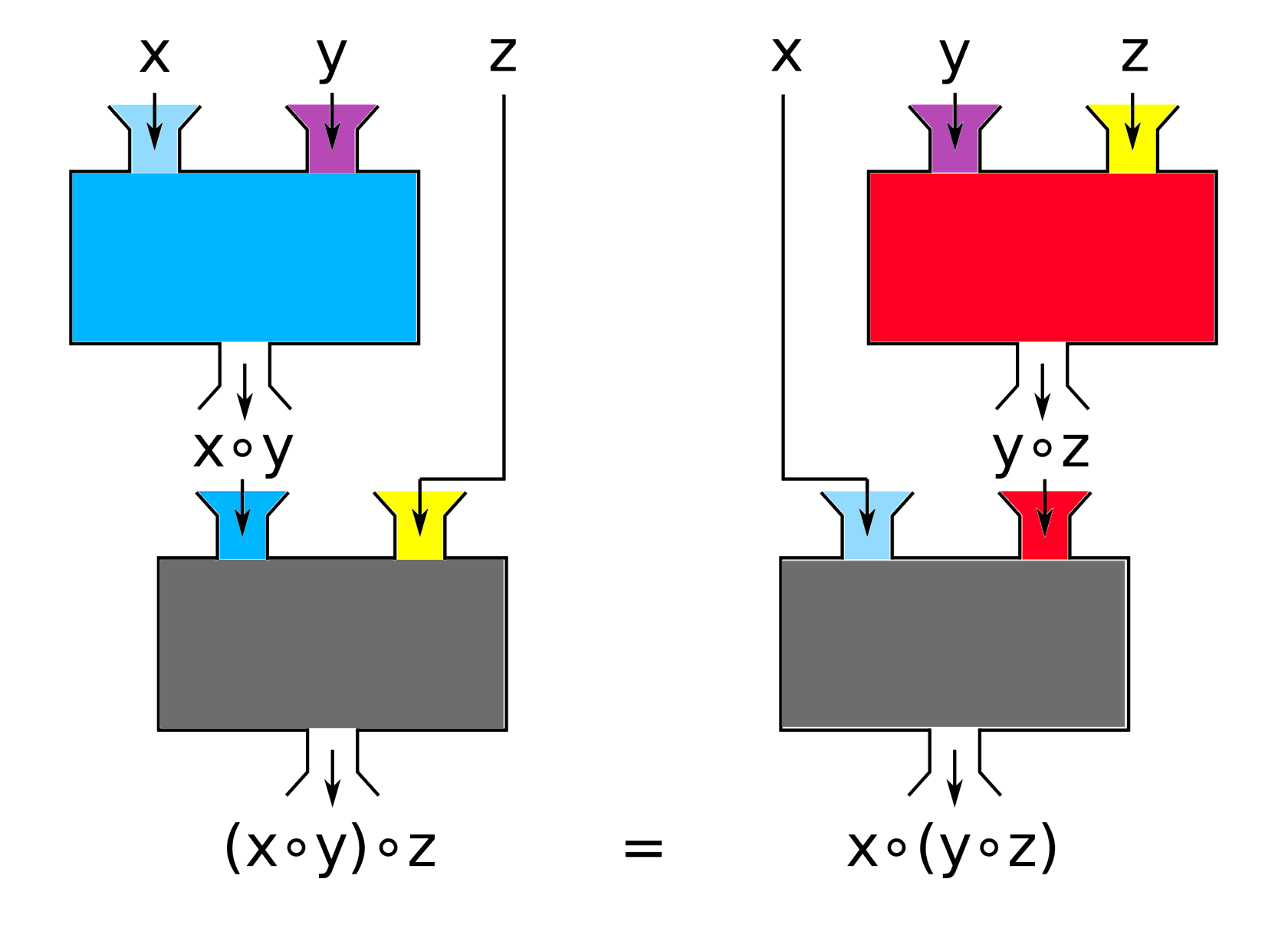
Термин ввёл Уильям Гамильтон в 1853 году.