Математический анализ - школьный курс
Решения задач по книге “Математический анализ в 57 школе” Давидович Б.М.
Вступительный комментарий: “эти решения я делал для себя, поэтому здесь много различных комментариев. Кому-то может показаться, что какие-то вещи расписаны излишне. На этот счёт я могу сказать, что у каждого разный уровень владения математикой: лично для меня такое “разжеванное” изложение на данный момент необходимо. Возможно вы найдете что-то для себя полезное или прокомментируете решения. Критика приветствуется! В задачах могут быть ошибки, будьте внимательны! ”
Теория множеств
Листок 1
Определение 1. Множества А и В называются равными (обозначение: А = В), если они состоят из одних и тех же элементов.
В дальнейшем вам необходимо будет доказать, что при равенстве множеств любой элемент множества A принадлежит множеству B и любой элемент множества B принадлежит множеству A.
В дальнейшем вам необходимо будет доказать, что при равенстве множеств любой элемент множества A принадлежит множеству B и любой элемент множества B принадлежит множеству A.
Определение 2. Множество А называется подмножеством множества В (обозначение: А ⊂ В), если каждый элемент, принадлежащий множеству А, принадлежит и множеству В (A ⊂ B ↔ ∀x(x ∈ A и x ∈ B).
Задача 1. Доказать, что для любых множеств А, В, С:
а) А ⊂ А б) если А ⊂ В и В ⊂ С, то А ⊂ С;
в) А = В, если и только если А ⊂ В и В ⊂ А.
а) А ⊂ А б) если А ⊂ В и В ⊂ С, то А ⊂ С;
в) А = В, если и только если А ⊂ В и В ⊂ А.
Решение а.
Доказать, что А ⊂ А.
По определению равенства множеств (определение 1) множества А и В называются равными (А = В), если они состоят из одних и тех же элементов. Очевидно, что множество А и множество А состоят из одних и тех же элементов, так как это одно и тоже множество (А = А).
По определению подмножества (определение 2), множество A является подмножеством множества B (A⊂B ), если каждый элемент x, принадлежащий A, принадлежит и B.
Поскольку A = A, то каждый элемент x, принадлежащий A, принадлежит самому множеству A (x∈A).
Следовательно А ⊂ А.
Попробуем так же доказать от противного.
Предположим, что А ⊄ А. Тогда по определению подмножества (определение 2) будет существовать такой x, что x ∈ A и x ∉ A. Мы пришли к противоречию: x одновременно принадлежит и не принадлежит А. Такого быть не может, следовательно наше предположение неверно и А ⊂ А.
Доказать, что А ⊂ А.
По определению равенства множеств (определение 1) множества А и В называются равными (А = В), если они состоят из одних и тех же элементов. Очевидно, что множество А и множество А состоят из одних и тех же элементов, так как это одно и тоже множество (А = А).
По определению подмножества (определение 2), множество A является подмножеством множества B (A⊂B ), если каждый элемент x, принадлежащий A, принадлежит и B.
Поскольку A = A, то каждый элемент x, принадлежащий A, принадлежит самому множеству A (x∈A).
Следовательно А ⊂ А.
Попробуем так же доказать от противного.
Предположим, что А ⊄ А. Тогда по определению подмножества (определение 2) будет существовать такой x, что x ∈ A и x ∉ A. Мы пришли к противоречию: x одновременно принадлежит и не принадлежит А. Такого быть не может, следовательно наше предположение неверно и А ⊂ А.
Вопрошающий
Для чего доказывать такие очевидные утверждения?
ОТВЕЧАЮЩИЙ:
Понимание того, что любое множество является подмножеством самого себя, на первый взгляд выглядит тривиально. Однако именно такие «самоочевидные» утверждения формируют прочный фундамент для будущего восприятия сложных математических структур и доказательств. В чём тут польза?
1. Формирование базового языка и интуиции.
Принятие факта, что «множество включено в себя» – это один из первых шагов к освоению формальной логики. Подобные утверждения обеспечивают "точку отсчёта" в цепочке более сложных рассуждений. Если вы уверенно оперируете базовыми свойствами, то при разборе сложных ситуаций у вас не возникает путаницы в базовых понятиях.
2. Верификация простейших свойств для дальнейших цепочек
рассуждений.
В теориях, где определяются отношения включения или частичного порядка, свойства рефлексивности (объект всегда находится в отношении к самому себе) – базовый кирпичик. На нём строится понимание того, как работают цепочки включений, вложенные множества или другие отношения. Зная, что каждый элементарный случай корректен, мы уменьшаем риск логической ошибки при расширении конструкции.
3. Подготовка к более сложным доказательствам.
В сложных доказательствах часто приходится ссылаться на тривиальные факты. Например, при доказательствах по индукции или при анализе иерархий множеств важно безоговорочно доверять базовым истинам, чтобы не застрять на начальных шагах. Понимание, что A есть подмножество A, исключает ненужные сомнения и упрощает переход к более тонким вопросам, таким как строгие подмножества (A ⊂ B при A ≠ B), пересечения, объединения и разные свойства отношений между множествами.
4. Формирование точности и дисциплины мышления.
Математика – точная наука. Привыкая к тому, что даже кажущиеся очевидными утверждения имеют точный смысл и место в логике, вы воспитываете в себе аккуратный подход к доказательствам. Это помогает не пропускать «мелочи», которые впоследствии могут оказаться важными при работе с более абстрактными теоремами.
Иными словами, знание того, что «A включено в A» – это не просто банальное утверждение, а фундаментальная «тренировка» логического взгляда на мир математических объектов. Чем увереннее вы владеете основными кирпичиками, тем легче вам потом строить из них математические «здания» любой сложности.
1. Формирование базового языка и интуиции.
Принятие факта, что «множество включено в себя» – это один из первых шагов к освоению формальной логики. Подобные утверждения обеспечивают "точку отсчёта" в цепочке более сложных рассуждений. Если вы уверенно оперируете базовыми свойствами, то при разборе сложных ситуаций у вас не возникает путаницы в базовых понятиях.
2. Верификация простейших свойств для дальнейших цепочек
рассуждений.
В теориях, где определяются отношения включения или частичного порядка, свойства рефлексивности (объект всегда находится в отношении к самому себе) – базовый кирпичик. На нём строится понимание того, как работают цепочки включений, вложенные множества или другие отношения. Зная, что каждый элементарный случай корректен, мы уменьшаем риск логической ошибки при расширении конструкции.
3. Подготовка к более сложным доказательствам.
В сложных доказательствах часто приходится ссылаться на тривиальные факты. Например, при доказательствах по индукции или при анализе иерархий множеств важно безоговорочно доверять базовым истинам, чтобы не застрять на начальных шагах. Понимание, что A есть подмножество A, исключает ненужные сомнения и упрощает переход к более тонким вопросам, таким как строгие подмножества (A ⊂ B при A ≠ B), пересечения, объединения и разные свойства отношений между множествами.
4. Формирование точности и дисциплины мышления.
Математика – точная наука. Привыкая к тому, что даже кажущиеся очевидными утверждения имеют точный смысл и место в логике, вы воспитываете в себе аккуратный подход к доказательствам. Это помогает не пропускать «мелочи», которые впоследствии могут оказаться важными при работе с более абстрактными теоремами.
Иными словами, знание того, что «A включено в A» – это не просто банальное утверждение, а фундаментальная «тренировка» логического взгляда на мир математических объектов. Чем увереннее вы владеете основными кирпичиками, тем легче вам потом строить из них математические «здания» любой сложности.
б) Доказать, что если А ⊂ В и В ⊂ С, то А ⊂ С
Пусть даны множества A, B и C такие, что A⊂B и B⊂C.
Для того чтобы показать A⊂C, нам необходимо доказать, что любой элемент множества A является также элементом множества C.
Пусть x∈A. Из условия A⊂B следует, что если x∈A, то x∈B.
Далее, так как B⊂C, то любой элемент множества B, в частности x, принадлежит также множеству C. Таким образом, если x∈A, то из цепочки включений A⊂B⊂C следует, что x∈C.
Итак, любой элемент множества A входит в множество C. Значит, выполнено включение A⊂C.
Следовательно, транзитивность отношения включения гарантирует, что если A⊂B и B⊂C, то обязательно A⊂C.
Пусть даны множества A, B и C такие, что A⊂B и B⊂C.
Для того чтобы показать A⊂C, нам необходимо доказать, что любой элемент множества A является также элементом множества C.
Пусть x∈A. Из условия A⊂B следует, что если x∈A, то x∈B.
Далее, так как B⊂C, то любой элемент множества B, в частности x, принадлежит также множеству C. Таким образом, если x∈A, то из цепочки включений A⊂B⊂C следует, что x∈C.
Итак, любой элемент множества A входит в множество C. Значит, выполнено включение A⊂C.
Следовательно, транзитивность отношения включения гарантирует, что если A⊂B и B⊂C, то обязательно A⊂C.
в) Доказать, что А = В, если и только если А ⊂ В и В ⊂ А.
(⇒) Пусть A = B. Тогда по определению равенства, множества состоят из одних и тех же элементов. Если они состоят из одних и тех же элементов, тогда по определению подмножеств каждый элемент множества A принадлежит множеству B, и наоборот: каждый элемент множества B принадлежит множеству A. Это означает одновременно A⊂B и B⊂A.
(⇐) Теперь предположим, что выполнены условия A⊂B и B⊂A. Это означает, что каждый элемент A содержится в B, и наоборот, каждый элемент B содержится в A. Следовательно, множества A и B имеют одни и те же элементы. По определению равенства множеств, это означает A=B.
Итак, мы показали, что равенство множеств эквивалентно взаимному включению. То есть:
A=B ⟺ (A⊂B и B⊂A).
(⇒) Пусть A = B. Тогда по определению равенства, множества состоят из одних и тех же элементов. Если они состоят из одних и тех же элементов, тогда по определению подмножеств каждый элемент множества A принадлежит множеству B, и наоборот: каждый элемент множества B принадлежит множеству A. Это означает одновременно A⊂B и B⊂A.
(⇐) Теперь предположим, что выполнены условия A⊂B и B⊂A. Это означает, что каждый элемент A содержится в B, и наоборот, каждый элемент B содержится в A. Следовательно, множества A и B имеют одни и те же элементы. По определению равенства множеств, это означает A=B.
Итак, мы показали, что равенство множеств эквивалентно взаимному включению. То есть:
A=B ⟺ (A⊂B и B⊂A).
б.1) Доказать, что A∪B = B∪A;
Доказательство равенства основывается на определении 1, в котором говорится, что множества равны тогда, когда они состоят из одних и тех же элементов: любой элемент множества A принадлежит множеству B и любой элемент множества B принадлежит множеству A.
Доказательство равенства основывается на определении 1, в котором говорится, что множества равны тогда, когда они состоят из одних и тех же элементов: любой элемент множества A принадлежит множеству B и любой элемент множества B принадлежит множеству A.
"Изначально моя интуиция мне говорила следующее: если в объединении важен только состав элементов, а не порядок записи множеств, тогда A∪B и B∪A должны иметь одинаковые элементы. Иначе говоря моя интуиция основывалось на том, что если множества по определению состоят из неповторяющихся элементов и порядок в них не имеет значения, тогда A∪B = B∪A. По духу оно верное, но это не математическое доказательство".
Необходимо доказать, что:
1) A∪B ⊂ B∪A ;
2) B∪A ⊂ A∪B.
1. Предположим, что A∪B ⊄ B∪A. В таком случае будет существовать такой x, что x ∈ A∪B
и x∉ B∪A. По определению объединением множеств A и B (обозначение: A∪B) называется множество, состоящее из таких x, что x ∈ A или x ∈ B. Если x ∈ A, то по определению объединения x ∈ B∪A. Если x ∈ B, то по определению объединения x ∈ B∪A. Мы пришли к противоречию: x ∈ B∪A и одновременно x∉ B∪A. Следовательно A∪B ⊂ B∪A.
2. Аналогично доказывается второе включение B∪A ⊂ A∪B. Предположим противное: B∪A ⊄ A∪B. Тогда должен существовать элемент x такой, что: x ∈ B∪A и x ∉ A∪B. Но если x ∈ B ∪ A, то по определению объединения: x ∈ B или x ∈ A. Если x ∈ B, то по определению объединения x ∈ A∪B. Если x ∈ A, то по определению объединения x ∈ A∪B. В любом случае получаем x ∈ A∪B. Противоречие: x ∈ A∪B и x ∉ A∪B одновременно. Значит, предположение неверно и B∪A ⊄ A∪B.
Так как доказаны оба включения: A∪B ⊂ B∪A и B∪A ⊂ A∪B, то по определению о равенстве множеств: A∪B = B∪A.
1) A∪B ⊂ B∪A ;
2) B∪A ⊂ A∪B.
1. Предположим, что A∪B ⊄ B∪A. В таком случае будет существовать такой x, что x ∈ A∪B
и x∉ B∪A. По определению объединением множеств A и B (обозначение: A∪B) называется множество, состоящее из таких x, что x ∈ A или x ∈ B. Если x ∈ A, то по определению объединения x ∈ B∪A. Если x ∈ B, то по определению объединения x ∈ B∪A. Мы пришли к противоречию: x ∈ B∪A и одновременно x∉ B∪A. Следовательно A∪B ⊂ B∪A.
2. Аналогично доказывается второе включение B∪A ⊂ A∪B. Предположим противное: B∪A ⊄ A∪B. Тогда должен существовать элемент x такой, что: x ∈ B∪A и x ∉ A∪B. Но если x ∈ B ∪ A, то по определению объединения: x ∈ B или x ∈ A. Если x ∈ B, то по определению объединения x ∈ A∪B. Если x ∈ A, то по определению объединения x ∈ A∪B. В любом случае получаем x ∈ A∪B. Противоречие: x ∈ A∪B и x ∉ A∪B одновременно. Значит, предположение неверно и B∪A ⊄ A∪B.
Так как доказаны оба включения: A∪B ⊂ B∪A и B∪A ⊂ A∪B, то по определению о равенстве множеств: A∪B = B∪A.
б.2) Доказать, что A∩B = B∩A;
Доказательство будем строить аналогично доказательству A∪B = B∪A.
Множество A∩B равно множеству B∩A тогда и только тогда, когда:
1) A∩B ⊂ B∩A ;
2) B∩A ⊂ A∩B.
Докажем, что: 1) A∩B ⊂ B∩A.
Предположим, что A∩B ⊄ B∩A. Тогда будет существовать хотя бы один x такой, что x ∈ A∩B и x ∉ B∩A. По определению пересечения, x ∈ A∩B означает, что x ∈ A и x ∈ B. Тогда, по определению B∩A, раз x ∈ B и x ∈ A, отсюда следует, что x ∈ B∩A. Мы пришли к противоречию: x ∈ B∩A и одновременно x∉ B∩A. Следовательно A∩B ⊂ B∩A.
Докажем, что: 1) B∩A ⊂ A∩B.
Предположим, что B∩A ⊄ A∩B. Тогда будет существовать хотя бы один x такой, что x ∈ B∩A и x ∉ A∩B. По определению пересечения, x ∈ B∩A означает, что x ∈ B и x ∈ A. Тогда, по определению A∩B, раз x ∈ A и x ∈ B, отсюда следует, что x ∈ A∩B. Мы пришли к противоречию: x ∈ A∩B и одновременно x∉ A∩B. Следовательно B∩A ⊂ A∩B.
Так как доказаны оба включения: A∩B ⊂ B∩A и B∩A ⊂ A∩B, то по определению о равенстве множеств: A∩B = B∩A.
Доказательство будем строить аналогично доказательству A∪B = B∪A.
Множество A∩B равно множеству B∩A тогда и только тогда, когда:
1) A∩B ⊂ B∩A ;
2) B∩A ⊂ A∩B.
Докажем, что: 1) A∩B ⊂ B∩A.
Предположим, что A∩B ⊄ B∩A. Тогда будет существовать хотя бы один x такой, что x ∈ A∩B и x ∉ B∩A. По определению пересечения, x ∈ A∩B означает, что x ∈ A и x ∈ B. Тогда, по определению B∩A, раз x ∈ B и x ∈ A, отсюда следует, что x ∈ B∩A. Мы пришли к противоречию: x ∈ B∩A и одновременно x∉ B∩A. Следовательно A∩B ⊂ B∩A.
Докажем, что: 1) B∩A ⊂ A∩B.
Предположим, что B∩A ⊄ A∩B. Тогда будет существовать хотя бы один x такой, что x ∈ B∩A и x ∉ A∩B. По определению пересечения, x ∈ B∩A означает, что x ∈ B и x ∈ A. Тогда, по определению A∩B, раз x ∈ A и x ∈ B, отсюда следует, что x ∈ A∩B. Мы пришли к противоречию: x ∈ A∩B и одновременно x∉ A∩B. Следовательно B∩A ⊂ A∩B.
Так как доказаны оба включения: A∩B ⊂ B∩A и B∩A ⊂ A∩B, то по определению о равенстве множеств: A∩B = B∩A.
в.1) Доказать, что A∪(B∪C)=(A∪B)∪C;
Доказательство иллюстрирует свойство ассоциативности операции объединения множеств. Ассоциативность объединения означает, что порядок группировки скобок не влияет на результат. Для доказательства требуется показать два включения:
1. Если х ∈ A, то по определению объединения х ∈ A∪B, тогда х ∈ (A∪B)∪C;
2. если х ∉ А, то х ∈ B∪C, тогда:
2.а. если х ∈ В, то х ∈ A∪B, тогда х ∈ (A∪B)∪C
2.б. если х ∈ С, то х ∈ (A∪B)∪C.
Во всех случаях A∪(B∪C) ⊂ (A∪B)∪C.
Шаг 2. (не буду расписывать полностью как первый шаг, ведь принцип и так понятен) Рассмотрим левую часть: (A∪B)∪C. Что это значит? Это значит, что любой произвольный элемент х ∈ A∪B или х ∈ C. Если х ∈ A∪B, то по определению объединения х ∈ (A∪B)∪C, если х ∉ А∪B, то х ∈ C, тогда х ∈ (A∪B)∪C. Следовательно, во всех случаях (A∪B)∪C ⊂ A∪(B∪C).
Доказательство иллюстрирует свойство ассоциативности операции объединения множеств. Ассоциативность объединения означает, что порядок группировки скобок не влияет на результат. Для доказательства требуется показать два включения:
- A∪(B∪C) ⊂ (A∪B)∪C;
- (A∪B)∪C ⊂ A∪(B∪C).
1. Если х ∈ A, то по определению объединения х ∈ A∪B, тогда х ∈ (A∪B)∪C;
2. если х ∉ А, то х ∈ B∪C, тогда:
2.а. если х ∈ В, то х ∈ A∪B, тогда х ∈ (A∪B)∪C
2.б. если х ∈ С, то х ∈ (A∪B)∪C.
Во всех случаях A∪(B∪C) ⊂ (A∪B)∪C.
Шаг 2. (не буду расписывать полностью как первый шаг, ведь принцип и так понятен) Рассмотрим левую часть: (A∪B)∪C. Что это значит? Это значит, что любой произвольный элемент х ∈ A∪B или х ∈ C. Если х ∈ A∪B, то по определению объединения х ∈ (A∪B)∪C, если х ∉ А∪B, то х ∈ C, тогда х ∈ (A∪B)∪C. Следовательно, во всех случаях (A∪B)∪C ⊂ A∪(B∪C).
в.2) Доказать, что A∩(B∩C)=(A∩B)∩C;
Доказательство иллюстрирует свойство ассоциативности операции объединения множеств. Ассоциативность объединения означает, что порядок группировки скобок не влияет на результат. Для доказательства требуется показать два включения:
Шаг 2. Производится аналогично. В конечном итоге мы получаем, что A∩(B∩C)=(A∩B)∩C.
Доказательство иллюстрирует свойство ассоциативности операции объединения множеств. Ассоциативность объединения означает, что порядок группировки скобок не влияет на результат. Для доказательства требуется показать два включения:
- A∩(B∩C) ⊂ (A∩B)∩C;
- (A∩B)∩C ⊂ A∩(B∩C).
Шаг 2. Производится аналогично. В конечном итоге мы получаем, что A∩(B∩C)=(A∩B)∩C.
г.1) Доказать, что A∩(B∪C)=(A∩B)∪(A∩C);
Решение сводится к тому, что нам требуется доказать включения, то есть:
1.A∩(B∪C) ⊂ (A∩B)∪(A∩C);
2.(A∩B)∪(A∩C) ⊂ A∩(B∪C).
Докажем первое включение.
Что означает A∩(B∪C)? Это означает, что в данном множестве есть некоторый x, такой, что х ∈ A и х ∈ В∪C. В свою очередь В∪C означает, что х ∈ В или х ∈ C. Получается, что х ∈ A и х ∈ В, или х ∈ A и х ∈ С.
Если x ∈ B, получаем x ∈ A∩B.
Если x ∈ C, получаем x ∈ A∩C.
Если мы посмотрим на правую часть, то очевидно, что это одно и тоже: x ∈ (A∩B)∪(A∩C). Так как множества равны, то A∩(B∪C)⊂(A∩B)∪(A∩C).
Докажем второе включение.
Что означает (A∩B)∪(A∩C)? Это означает, что х ∈ А или х ∈ В и х ∈ А или х ∈ С. Рассмотрим правую часть A∩(B∪C). Это означает, что х ∈ А или х ∈ В и х ∈ А или х ∈ С. Очевидно, что они равны и по определению равенства (A∩B)∪(A∩C)⊂A∩(B∪C).
Решение сводится к тому, что нам требуется доказать включения, то есть:
1.A∩(B∪C) ⊂ (A∩B)∪(A∩C);
2.(A∩B)∪(A∩C) ⊂ A∩(B∪C).
Докажем первое включение.
Что означает A∩(B∪C)? Это означает, что в данном множестве есть некоторый x, такой, что х ∈ A и х ∈ В∪C. В свою очередь В∪C означает, что х ∈ В или х ∈ C. Получается, что х ∈ A и х ∈ В, или х ∈ A и х ∈ С.
Если x ∈ B, получаем x ∈ A∩B.
Если x ∈ C, получаем x ∈ A∩C.
Если мы посмотрим на правую часть, то очевидно, что это одно и тоже: x ∈ (A∩B)∪(A∩C). Так как множества равны, то A∩(B∪C)⊂(A∩B)∪(A∩C).
Докажем второе включение.
Что означает (A∩B)∪(A∩C)? Это означает, что х ∈ А или х ∈ В и х ∈ А или х ∈ С. Рассмотрим правую часть A∩(B∪C). Это означает, что х ∈ А или х ∈ В и х ∈ А или х ∈ С. Очевидно, что они равны и по определению равенства (A∩B)∪(A∩C)⊂A∩(B∪C).
Задача выше иллюстрирует распределительный закон в логике. Ниже приведен рассказ, иллюстрирующий его.
Рассказ о хитроумной герцогине.
В одном далёком королевстве жила герцогиня Изабелла, известная своим умом и любовью к сложным задачам. Однажды король Артемий поручил ей необычное задание: нужно было выбрать из трёх сотен подданных самых достойных, которые могли бы служить при дворе.
Король поставил два жёстких критерия:
— Я ищу тех, кто или смелый, или умный, но обязательно должен быть лояльным ко мне. Если вы считаете, что подходите, приходите ко мне для испытания.
Испытание герцогини было хитроумным. Она решила применить распределительный закон, хотя, конечно, сама этого так не называла. Она мысленно разделила задачу на два этапа:
И тогда, размышляя, она поняла: тех, кто одновременно смел и лоялен, она уже нашла. Тех, кто умён и лоялен, тоже. Все эти люди составляют её союзников. И проверять больше нечего — те, кто прошли хотя бы одно испытание, уже подходят.
К утру герцогиня огласила свой выбор. Люди толпились во дворе замка, а Изабелла вышла к ним с итогами. Она объявила:
— Если ты или смел, или умён, но при этом лоялен мне, значит, ты мой союзник. И, конечно, если ты оказался смелым и лояльным — я взяла тебя. Если ты умён и лоялен — ты тоже здесь. И я не упустила никого, кто подходит!
Этот рассказ иллюстрирует, как распределительный закон помогает разложить задачу на более простые части. Условие "лояльный и (смелый или умный)" распределяется на две группы: "лояльный и смелый" и "лояльный и умный". А объединение этих групп полностью покрывает всех подходящих кандидатов.
В одном далёком королевстве жила герцогиня Изабелла, известная своим умом и любовью к сложным задачам. Однажды король Артемий поручил ей необычное задание: нужно было выбрать из трёх сотен подданных самых достойных, которые могли бы служить при дворе.
Король поставил два жёстких критерия:
- Человек должен быть смелым или умным.
- При этом он обязательно должен быть лояльным герцогине.
— Я ищу тех, кто или смелый, или умный, но обязательно должен быть лояльным ко мне. Если вы считаете, что подходите, приходите ко мне для испытания.
Испытание герцогини было хитроумным. Она решила применить распределительный закон, хотя, конечно, сама этого так не называла. Она мысленно разделила задачу на два этапа:
- Проверить всех, кто смел, но также проверить их лояльность.
- Проверить всех, кто умён, и тоже убедиться в их лояльности.
И тогда, размышляя, она поняла: тех, кто одновременно смел и лоялен, она уже нашла. Тех, кто умён и лоялен, тоже. Все эти люди составляют её союзников. И проверять больше нечего — те, кто прошли хотя бы одно испытание, уже подходят.
К утру герцогиня огласила свой выбор. Люди толпились во дворе замка, а Изабелла вышла к ним с итогами. Она объявила:
— Если ты или смел, или умён, но при этом лоялен мне, значит, ты мой союзник. И, конечно, если ты оказался смелым и лояльным — я взяла тебя. Если ты умён и лоялен — ты тоже здесь. И я не упустила никого, кто подходит!
Этот рассказ иллюстрирует, как распределительный закон помогает разложить задачу на более простые части. Условие "лояльный и (смелый или умный)" распределяется на две группы: "лояльный и смелый" и "лояльный и умный". А объединение этих групп полностью покрывает всех подходящих кандидатов.
г.2) Доказать, что A∪(B∩C)=(A∪B)∩(A∪C);
Для доказательства равенства по определению равенства множеств, решение сводится к тому, что нам требуется доказать два включения, то есть:
1.A∪(B∩C)⊂(A∪B)∩(A∪C);
2.(A∪B)∩(A∪C)⊂A∪(B∩C).
Докажем первое включение.
Что означает A∪(B∩C)? Это означает, что в данном множестве есть некоторый x, такой, что х ∈ A или х ∈ В∩C. В свою очередь В∩C означает, что х ∈ В и х ∈ C. Получается, что х ∈ A или х ∈ В и х ∈ A или х ∈ С.
Если мы посмотрим на правую часть, то очевидно, что это одно и тоже: x ∈ (A∪B)∩(A∪C). Так как множества равны, то A∪(B∩C)⊂(A∪B)∩(A∪C).
Докажем второе включение.
Что означает (A∪B)∩(A∪C)? Это означает, что х ∈ А или х ∈ В и х ∈ А или х ∈ С.
Рассмотрим правую часть A∩(B∪C). Это означает, что х ∈ А или х ∈ В и х ∈ А или х ∈ С. Очевидно, что они равны и по определению равенства (A∩B)∪(A∩C)⊂A∩(B∪C).
Мы доказали оба включения, следовательно A∪(B∩C)=(A∪B)∩(A∪C).
Для доказательства равенства по определению равенства множеств, решение сводится к тому, что нам требуется доказать два включения, то есть:
1.A∪(B∩C)⊂(A∪B)∩(A∪C);
2.(A∪B)∩(A∪C)⊂A∪(B∩C).
Докажем первое включение.
Что означает A∪(B∩C)? Это означает, что в данном множестве есть некоторый x, такой, что х ∈ A или х ∈ В∩C. В свою очередь В∩C означает, что х ∈ В и х ∈ C. Получается, что х ∈ A или х ∈ В и х ∈ A или х ∈ С.
Если мы посмотрим на правую часть, то очевидно, что это одно и тоже: x ∈ (A∪B)∩(A∪C). Так как множества равны, то A∪(B∩C)⊂(A∪B)∩(A∪C).
Докажем второе включение.
Что означает (A∪B)∩(A∪C)? Это означает, что х ∈ А или х ∈ В и х ∈ А или х ∈ С.
Рассмотрим правую часть A∩(B∪C). Это означает, что х ∈ А или х ∈ В и х ∈ А или х ∈ С. Очевидно, что они равны и по определению равенства (A∩B)∪(A∩C)⊂A∩(B∪C).
Мы доказали оба включения, следовательно A∪(B∩C)=(A∪B)∩(A∪C).
Ниже приведен рассказ, иллюстрирующий отношения множеств выше.
Мудрец и старинный архив.
В одном далёком городе был старинный архив – величайшее собрание мудростей, преданий и тайн. Каждый год в него разрешалось войти лишь немногим избранным. Хранитель архива, престарелый мудрец, имел свои строгие правила, по которым решал, кто сможет переступить порог.
Сначала он говаривал: «В архив пустим всех настоящих мудрецов – тех, кто известен своим глубоким знанием и светлым умом. Также я приму тех, кто одновременно и силён духом, и честен сердцем, ведь такая редкая совокупность качеств очень ценна для понимания истинных тайн». Таким образом, он выдвигал одно простое условие: в архив попадут либо мудрецы, либо те, кто обладает и силой духа, и честностью одновременно.
Однако, к нему иногда приходили посланцы издалека и просили объяснить его логику более доступно. Тогда мудрец говорил: «Посмотрите иначе. Если вы не мудрец, но хотите войти, вам понадобится хотя бы одна из двух вещей – или способность искренне говорить правду, или умение преодолеть страх (то есть честность или силу духа). Но и этого мало. Чтобы действительно войти, нужно не просто иметь одну из этих добродетелей вместе с мудростью. Вам нужно, чтобы сочетание ваших качеств позволяло вам быть либо мудрым или сильным, и одновременно – либо мудрым или честным. Иначе говоря, одни только сила или честность без второго из этих качеств вам не помогут. Но если вы – мудрец, то вам даже не нужно об этом беспокоиться. Вы и так прошли испытание».
Когда гость пытался разобраться, он замечал любопытную закономерность:
В одном далёком городе был старинный архив – величайшее собрание мудростей, преданий и тайн. Каждый год в него разрешалось войти лишь немногим избранным. Хранитель архива, престарелый мудрец, имел свои строгие правила, по которым решал, кто сможет переступить порог.
Сначала он говаривал: «В архив пустим всех настоящих мудрецов – тех, кто известен своим глубоким знанием и светлым умом. Также я приму тех, кто одновременно и силён духом, и честен сердцем, ведь такая редкая совокупность качеств очень ценна для понимания истинных тайн». Таким образом, он выдвигал одно простое условие: в архив попадут либо мудрецы, либо те, кто обладает и силой духа, и честностью одновременно.
Однако, к нему иногда приходили посланцы издалека и просили объяснить его логику более доступно. Тогда мудрец говорил: «Посмотрите иначе. Если вы не мудрец, но хотите войти, вам понадобится хотя бы одна из двух вещей – или способность искренне говорить правду, или умение преодолеть страх (то есть честность или силу духа). Но и этого мало. Чтобы действительно войти, нужно не просто иметь одну из этих добродетелей вместе с мудростью. Вам нужно, чтобы сочетание ваших качеств позволяло вам быть либо мудрым или сильным, и одновременно – либо мудрым или честным. Иначе говоря, одни только сила или честность без второго из этих качеств вам не помогут. Но если вы – мудрец, то вам даже не нужно об этом беспокоиться. Вы и так прошли испытание».
Когда гость пытался разобраться, он замечал любопытную закономерность:
- Если человек – мудрец, его пропускают.
- Если нет, он должен быть и сильным, и честным одновременно, чтобы пройти.
- Неважно, какой путь рассуждения выбрать – в итоге двери открываются для тех же самых людей: мудрецов и для тех редких, кто сочетает в себе сразу две другие добродетели.
- А если пытаться идти обходными тропами, думать сначала о силе и мудрости, а потом о мудрости и честности, результат всё равно будет один и тот же. Как бы не усложнять задачу, круг избранных не изменится.
Определение 6. Разностью множеств A и B (обозначение: A\B) называется множество, состоящее из таких x, что x∈A и x∉B.
З . Верно ли, что для любых множеств A, B,C
а) (A\B)∪B=A; б) A\(A\B)=A∩B;
в) A\(B∪C)=(A\B)∩(A\C); г) A\(B∩C)=(A\B)∪(A\C);
д) A\(B\C)=(A\B)∪(A∩C); е) (A\B)∪(B\A)=A∪B?
а) (A\B)∪B=A; б) A\(A\B)=A∩B;
в) A\(B∪C)=(A\B)∩(A\C); г) A\(B∩C)=(A\B)∪(A\C);
д) A\(B\C)=(A\B)∪(A∩C); е) (A\B)∪(B\A)=A∪B?
а) Верно ли, что (A\B) ∪ B = A;
С первого взгляда может показаться, что равенство неверное. Ведь если попробовать подставить какие-либо значения, то станет очевидно почему. Например:
А = {1,2,3,4}, B = {3,4,5,6}.
Тогда:
1) A\B = {1,2}.
2) {1,2} ∪ {3,4,5,6} = {1,2,3,4,5,6}.
Как видно, итоговое множество не равно А.
Но если рассмотреть другой пример:
А = {1,2,3,4}, B = {3,4}.
В данном случае B⊂A. Тогда:
1) A\B = {1,2}.
2) {1,2} ∪ {3,4} = {1,2,3,4}.
Получится, что равенство верное и (A\B) ∪ B = A.
Мы можем сделать предположение, что (A\B) ∪ B = A тогда и только тогда, когда B⊂A. В противном случае равенство не верное.
Доказательство нужно выполнить в два этапа. На первом этапе показать, что:
Если B⊄A, то (A∖B) ∪ B ≠ A.
Второй этап:
Если B⊂A, то (A∖B) ∪ B = A.
Первый этап:
Если B⊄A, то (A∖B) ∪ B ≠ A.
Пусть B не является подмножеством A. Это значит, что существует элемент x ∈ B x ∉ A.
Например в примере выше: А = {1,2,3,4}, B = {3,4,5,6}. Элементы 5 и 6 в множестве В принадлежат В, но не принадлежат А.
Рассмотрим теперь множество (A∖B) ∪ B. Поскольку x ∈ B, очевидно, что x ∈ (A∖B) ∪ B. Значит, в левой части равенства присутствует элемент x, которого нет в A.
При B⊄A, (A∖B) ∪ B ≠ A.
Второй этап:
Делаем вывод, что равенство верное тогда и только тогда, когда B⊂A. Для доказательства равенства (A∖B) ∪ B = A необходимо показать два включения:
1) (A∖B) ∪ B ⊂ A;
2) A ⊂ (A∖B) ∪ B.
1) Первое включение A ⊂ (A∖B) ∪ B: возьмём произвольный элемент x ∈ A.
Объединяя результаты, получаем равенство: (A∖B) ∪ B = A, при условии что B ⊂ A.
С первого взгляда может показаться, что равенство неверное. Ведь если попробовать подставить какие-либо значения, то станет очевидно почему. Например:
А = {1,2,3,4}, B = {3,4,5,6}.
Тогда:
1) A\B = {1,2}.
2) {1,2} ∪ {3,4,5,6} = {1,2,3,4,5,6}.
Как видно, итоговое множество не равно А.
Но если рассмотреть другой пример:
А = {1,2,3,4}, B = {3,4}.
В данном случае B⊂A. Тогда:
1) A\B = {1,2}.
2) {1,2} ∪ {3,4} = {1,2,3,4}.
Получится, что равенство верное и (A\B) ∪ B = A.
Мы можем сделать предположение, что (A\B) ∪ B = A тогда и только тогда, когда B⊂A. В противном случае равенство не верное.
Доказательство нужно выполнить в два этапа. На первом этапе показать, что:
Если B⊄A, то (A∖B) ∪ B ≠ A.
Второй этап:
Если B⊂A, то (A∖B) ∪ B = A.
Первый этап:
Если B⊄A, то (A∖B) ∪ B ≠ A.
Пусть B не является подмножеством A. Это значит, что существует элемент x ∈ B x ∉ A.
Например в примере выше: А = {1,2,3,4}, B = {3,4,5,6}. Элементы 5 и 6 в множестве В принадлежат В, но не принадлежат А.
Рассмотрим теперь множество (A∖B) ∪ B. Поскольку x ∈ B, очевидно, что x ∈ (A∖B) ∪ B. Значит, в левой части равенства присутствует элемент x, которого нет в A.
- (A∖B)∪B содержит;
- A не содержит x.
При B⊄A, (A∖B) ∪ B ≠ A.
Второй этап:
Делаем вывод, что равенство верное тогда и только тогда, когда B⊂A. Для доказательства равенства (A∖B) ∪ B = A необходимо показать два включения:
1) (A∖B) ∪ B ⊂ A;
2) A ⊂ (A∖B) ∪ B.
1) Первое включение A ⊂ (A∖B) ∪ B: возьмём произвольный элемент x ∈ A.
- Если x ∈ B, тогда очевидно x ∈ (A∖B) ∪ B.
- Если x ∉ B, тогда x ∈ A, а значит x ∈ (A∖B) ∪ B.
- В любом случае x ∈ (A∖B) ∪ B, значит A \ (A\B) = A ∩ B (A∖B) ∪ B.
- Либо x ∈ A∖B, тогда по определению x ∈ A.
- Либо x ∈ B. Поскольку мы предположили B⊂A, из этого следует, что x∈A.
Объединяя результаты, получаем равенство: (A∖B) ∪ B = A, при условии что B ⊂ A.
б) Верно ли, что A \ (A\B) = A ∩ B;
Для большей простоты и наглядности давайте разберем в начале пример, в котором B ⊄ A:
А = {1,2,3,4}, B = {3,4,5,6}.
Тогда:
1) A\B = {1,2,3,4}\{3,4,5,6} = {1,2}.
2) A\ (A\B) = {1,2,3,4} \ {1,2} = {3,4}.
3) A ∩ B = {1,2,3,4} ∩ {3,4,5,6} = {3,4}.
В таком случае равенство верное: A \ (A\B) = A ∩ B.
Рассмотрим случай когда B ⊂ A:
А = {1,2,3,4}, B = {3,4}.
Тогда:
1) A\B = {1,2,3,4}\{3,4} = {1,2}.
2) A\ (A\B) = {1,2,3,4} \ {1,2} = {3,4}.
3) A ∩ B = {1,2,3,4} ∩ {3,4,5,6} = {3,4}.
В таком случае равенство так же верное: A \ (A\B) = A ∩ B.
И так. На первый взгляд кажется, что выражение верное. Однако оно требует строгого формального доказательства. Доказательство производим через оба включения. Необходимо доказать, что:
1) A \ (A\B) ⊂ A ∩ B;
2) A ∩ B ⊂ A \ (A\B).
Для большей простоты и наглядности давайте разберем в начале пример, в котором B ⊄ A:
А = {1,2,3,4}, B = {3,4,5,6}.
Тогда:
1) A\B = {1,2,3,4}\{3,4,5,6} = {1,2}.
2) A\ (A\B) = {1,2,3,4} \ {1,2} = {3,4}.
3) A ∩ B = {1,2,3,4} ∩ {3,4,5,6} = {3,4}.
В таком случае равенство верное: A \ (A\B) = A ∩ B.
Рассмотрим случай когда B ⊂ A:
А = {1,2,3,4}, B = {3,4}.
Тогда:
1) A\B = {1,2,3,4}\{3,4} = {1,2}.
2) A\ (A\B) = {1,2,3,4} \ {1,2} = {3,4}.
3) A ∩ B = {1,2,3,4} ∩ {3,4,5,6} = {3,4}.
В таком случае равенство так же верное: A \ (A\B) = A ∩ B.
И так. На первый взгляд кажется, что выражение верное. Однако оно требует строгого формального доказательства. Доказательство производим через оба включения. Необходимо доказать, что:
1) A \ (A\B) ⊂ A ∩ B;
2) A ∩ B ⊂ A \ (A\B).

- A \ (A\B) ⊂ A ∩ B
x ∈ A∖(A∖B) ⟺ (x ∈ A)∧(x ∉ (A∖B)).
С первым условием правой части всё понятно: x ∈ A. Давайте рассмотрим вторую часть справа — x ∉ (A∖B):
x ∉ (A∖B) ⟺ ¬(x ∈ A и x ∉ B) ⟺ (x ∉ A) или (x ∈ B).Здесь следует добавить, что ¬(x ∈ A и x ∉ B) ⟺ (x ∉ A) или (x ∈ B) следует из логических законов де Моргана. Например:
1) ¬ (P ∧ Q) ≡ (¬ P) ∨ (¬ Q)
Отрицание конъюнкции (логического «и») превращается в дизъюнкцию (логическое «или») отрицаний.
2) ¬ (P ∨ Q) ≡ (¬ P) ∧ (¬ Q)
Отрицание дизъюнкции (логического «или») превращается в конъюнкцию (логическое «и») отрицаний.
1) ¬ (P ∧ Q) ≡ (¬ P) ∨ (¬ Q)
Отрицание конъюнкции (логического «и») превращается в дизъюнкцию (логическое «или») отрицаний.
2) ¬ (P ∨ Q) ≡ (¬ P) ∧ (¬ Q)
Отрицание дизъюнкции (логического «или») превращается в конъюнкцию (логическое «и») отрицаний.
Так как мы уже знаем, что x ∈ A, возможность x ∉ A исключается. Остаётся только x ∈ B.
Итак, мы имеем x ∈ A и x ∈ B. Следовательно:
x ∈ A∩B.
Поскольку x был взят произвольно, мы показали, что любой элемент из A∖(A∖B) принадлежит A∩B. Отсюда:
A∖(A∖B) ⊂ A∩B.
2. A∩B ⊂ A∖(A∖B)
Возьмём произвольный элемент x ∈ A∩B. Тогда:
x ∈ A и x ∈ B.
Рассмотрим множество A∖B. Поскольку x ∈ B, очевидно x ∉ (A∖B), так как A∖B содержит элементы из A, которые не принадлежат B. Таким образом:
x ∈ A, x ∉ (A∖B).
Это означает, что:
x ∈ A∖(A∖B).
Так как x был произвольным элементом из A∩B, мы получили:
Итак, мы имеем x ∈ A и x ∈ B. Следовательно:
x ∈ A∩B.
Поскольку x был взят произвольно, мы показали, что любой элемент из A∖(A∖B) принадлежит A∩B. Отсюда:
A∖(A∖B) ⊂ A∩B.
2. A∩B ⊂ A∖(A∖B)
Возьмём произвольный элемент x ∈ A∩B. Тогда:
x ∈ A и x ∈ B.
Рассмотрим множество A∖B. Поскольку x ∈ B, очевидно x ∉ (A∖B), так как A∖B содержит элементы из A, которые не принадлежат B. Таким образом:
x ∈ A, x ∉ (A∖B).
Это означает, что:
x ∈ A∖(A∖B).
Так как x был произвольным элементом из A∩B, мы получили:
- A∩B⊂A∖(A∖B)
Я немного подумал и решил, что можно попробовать доказать такой случай:
Доказать, что A \ А = ∅.
Предположим, что A \ А ≠ ∅. По определению разностью множеств A и B (обозначение: A\B) называется множество, состоящее из таких x, что x ∈ A и x ∉ B. В результате получится такой х, что x ∈ A и x ∉ А. Такого х существовать не может, потому что х либо принадлежит одному множеству, либо не принадлежит ему. В результате остается только пустое множество ∅. Поэтому A \ А = ∅.
Доказать, что A \ А = ∅.
Предположим, что A \ А ≠ ∅. По определению разностью множеств A и B (обозначение: A\B) называется множество, состоящее из таких x, что x ∈ A и x ∉ B. В результате получится такой х, что x ∈ A и x ∉ А. Такого х существовать не может, потому что х либо принадлежит одному множеству, либо не принадлежит ему. В результате остается только пустое множество ∅. Поэтому A \ А = ∅.
в) A\(B∪C) = (A\B) ∩ (A\C);
Возьмем произвольные множества: А = {1,2,3,4}, B = {3,4,5,6}, С = {5,6,7,8}.
Левая часть: A\(B∪C).
A\(B∪C) ⊂ (A\B) ∩ (A\C).
Левая часть A\(B∪C):
x ∈ A и x ∉ (B∪C).
Что значит x ∉ (B∪C)?
Возьмем произвольные множества: А = {1,2,3,4}, B = {3,4,5,6}, С = {5,6,7,8}.
Левая часть: A\(B∪C).
- B∪C = {3,4,5,6,7,8}
- A\(B∪C) = {1,2,3,4}\{3,4,5,6,7,8} = {1,2}.
- A\B = {1,2,3,4}\{3,4,5,6} = {1,2}
- A\C = {1,2,3,4}\{5,6,7,8} = {1,2,3,4}
- (A\B) ∩ (A\C) = {1,2} ∩ {1,2,3,4} = {1,2}
A\(B∪C) ⊂ (A\B) ∩ (A\C).
Левая часть A\(B∪C):
x ∈ A и x ∉ (B∪C).
Что значит x ∉ (B∪C)?
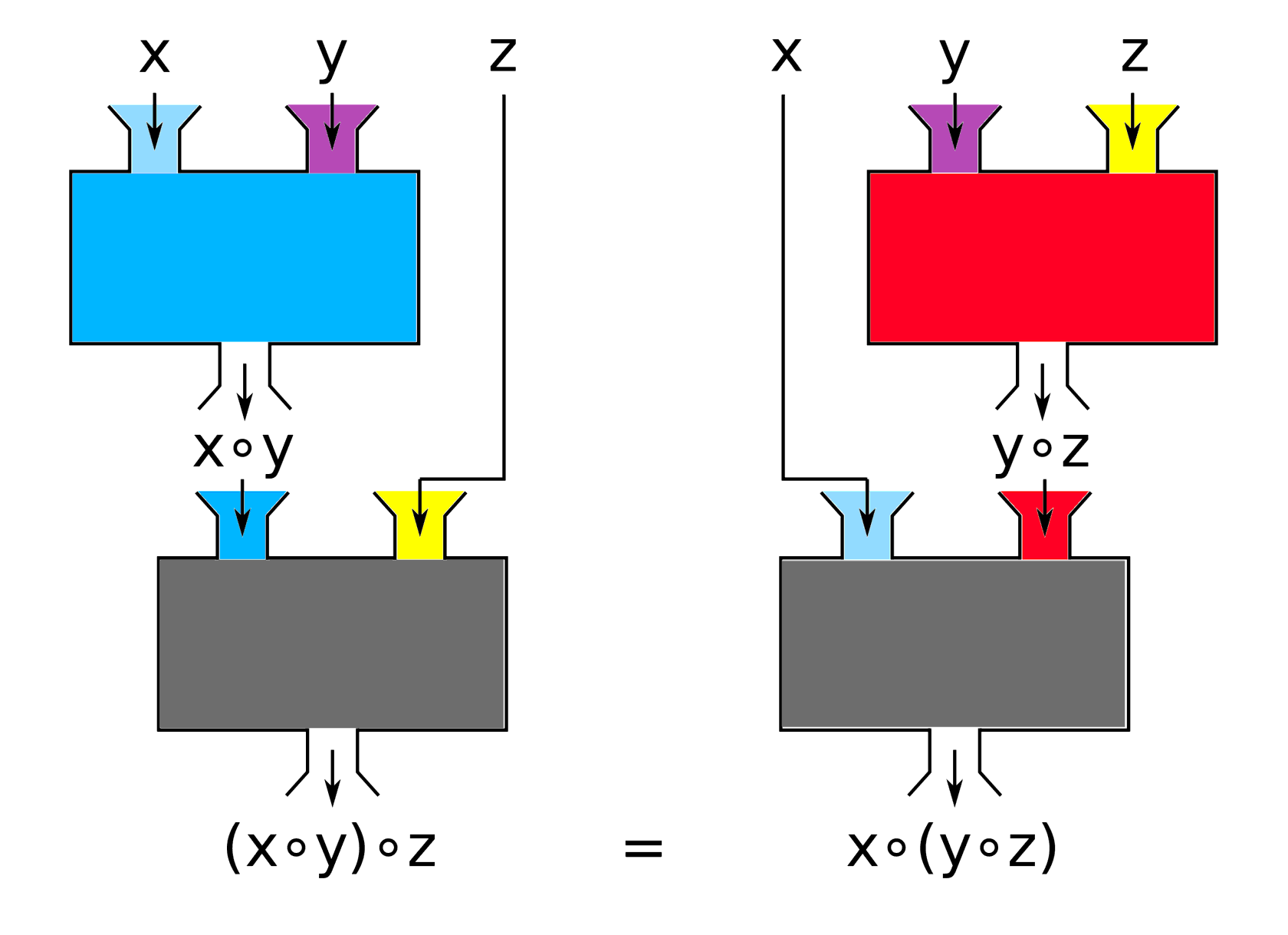
Ассоциативность
Ассоциати́вность (сочетательность) — свойство бинарной операции ∘, заключающееся в возможности осуществлять последовательное применение формулы (x∘y)∘z=x∘(y∘z) в произвольном порядке к элементам x,y,z.
Термин ввёл Уильям Гамильтон в 1853 году.
Термин ввёл Уильям Гамильтон в 1853 году.